Integrated Nested Laplace Approximation (INLA)

Astrophysical processes operate across a rich hierarchy of physical scales through time and space; the coupling between them giving rise to an intimate bond between the evolutionary histories of the smallest and largest structures. This interplay between local and global dynamics is manifest in the observed morphologies of extended astronomical sources, most notably galaxies.

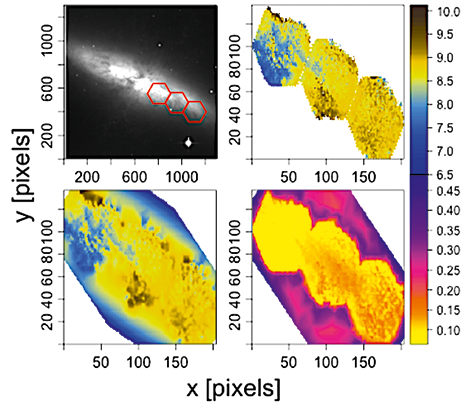
Traditionally, stellar population properties are obtained from IFU cubes using spectrum fitting codes in which each spaxel is treated independently. In neglecting the spatial information of the IFU data and the expectation of astrophysical and/or instrumental correlations between measured values at nearby locations—these approaches may fail to extract the complete signal from its noisy background.

This problem has been recognized before and several attempts to include spatial information have been made. The most common of these adaptive binning techniques is Voronoi tessellation. Although segmentation approaches boost the statistical confidence of the spectral analysis, they do so at the expense of spatial precision (e.g Cid Fernandes et al. 2014), and may lead to biased estimates if the averaged regions are inhomogeneous.

To overcome the limitations of segmentation-based approaches, this work introduces a model to evaluate the spatial information encoded in the IFU spectra. The method relies on the use of Gaussian Markov Random Fields (GMRF) to estimate the unobserved spatial field and is built under a hierarchical Bayesian framework to learn the spatial correlation structure as part of the model fitting. For fast Bayesian inference, the model is implemented using the Integrated Nested Laplace Approximation (INLA) framework.

This project is a result from COIN Residence Program #4 – Clermont Ferrand, France/2017.

Full citation: Gonzalez-Gaitan et al., 2019, MNRAS, 482 (3), 3880–3891